Building a random quote machine with Redux
This is Part 4 of the Making a random quote machine in a few different flavors series.
You can read more about this project’s background on the project’s page. Or start from the beginning with part 1 of this series.
If you’re curious about the next flavors, you should subscribe to Morse Wall. I think you’ll like it a lot!
In flavor #3, the data (quotes) is requested from a REST API.
In this flavor, I have the data inside an array stored inside a JavaScript module part of the project and I’m using state management (with Redux) to help me update the different UI elements with the current application state.
These are the different flavors that are part of this series:
- HTML + CSS + Vanilla JS + quotes array
- HTML + CSS + Vanilla JS + JSON with quotes (members-only post)
- HTML + CSS + Vanilla JS + quotes REST API
HTML + Vanilla JS + SAAS + quotes array(nah, because let’s be opinionated about SASS)HTML + Vanilla JS + Bootstrap + quotes array(nah, because let’s be opinionated about Bootstrap)HTML + CSS + JQuery + JSON with quotes(nah, because let’s be opinionated about JQuery)- HTML + CSS + Redux + quotes array (this flavor)
HTML + CSS + Redux + JQuery + JSON with quotes(nah, because let’s be opinionated about JQuery)- HTML + CSS + Redux + Redux Thunk + JSON with quotes
- HTML + CSS + React + quotes array
- HTML + CSS + React + JSON with quotes (members-only post)
- HTML + CSS + React Hooks + quotes array
- HTML + CSS + React Hooks + JSON with quotes (members-only post)
HTML + CSS + React + React Redux + quotes array(nah, because let’s be bullish about writing any new components with React Hooks)HTML + CSS + React + React Redux + Redux Thunk + JSON with quotes(nah, because let’s be bullish about writing any new components with React Hooks)- HTML + CSS + React Hooks + React Redux + quotes array
- HTML + CSS + React Hooks + React Redux + Redux Thunk + JSON with quotes
HTML + CSS + React Hooks + React Redux Hooks + quotes array(nah, because let’s be opinionated about React Redux Hooks)HTML + CSS + React Hooks + React Redux Hooks + Redux Thunk + JSON with quote(nah, because let’s be opinionated about React Redux Hooks)
In Part 5 (to be posted next week), I will cover a fifth flavor and will using Redux Thunk to call an asynchronous endpoint as the data (quotes) is requested from an external resource.
If you’re curious about the next flavors and would like to make a writer very happy today, you should subscribe to Morse Wall.
State management? Why overcomplicate?
Why am I overcomplicating a really simple application that can be shipped in 3 lines of functional Vanilla JavaScript? Because:
True that...
There are always (at least) two ways to solve a problem. One is faster, the other you just don’t know yet.
The above is the spirit behind the Making a random quote machine in a few different flavors series. And with that in mind, there is no better way to practice a new way to solve a problem than to ship a simple app in a simpler environment with fewer moving parts. Enjoy!
What is state ?
State is the “situation” the application is currently in. To exemplify, a few of the many states a given application can be in, at any moment, are for instance:
- loaded;
- not loaded;
- logged-in;
- not logged-in;
- hamburger navigation menu open;
- hamburger navigation menu closed;
- etc.
For this random quote machine application, the state stores a piece of data, a random quote that gets selected when the application runs. This state (random quote) is then listened to and different UI elements are updated with it.
The GIF below shows the state changing following a certain action-event in the application.

As a note, to track state (as per gif above), I use Redux DevTools Extension to time travel in the application’s state. The extension records dispatched actions (more on dispatched actions below in the article) and the state of the Redux store (more on the store further down) at every point in time. This allows me to inspect the state and travel back in time to a previous application state without reloading the page.
Flavor #4: HTML + CSS + Redux + quotes array in JS module
First things first, the data is stored in a JavaScript module. Because good software developers divide their code into modules, right? In other words, unlike previous flavors in this series (all JS code was previously inside a single file), there are a number of JavaScript files in this flavor.
Like previously, there is a tiny number of quotes in the code snippet below (so I can illustrate the point), but many more quotes in the array in production.
The getRandomQuote function spits out a random quote from the quotes array. I then export getRandomQuote so I can use it in another JS module.
//getRandomQuote.js
//defining function that accesses random quote from quotes array, making it a JS function/module
const getRandomQuote = () => {
//defining an array for the quotes, wrapping it inside a JS function/module
const quotes = [
{
quoteText:
'"Many of you appear concerned that we are wasting valuable lesson time, but I assure you we will go back to school the moment you start listening to science and give us a future."',
quoteAuthor: "@GretaThunberg",
},
{
quoteText:
'"I was fortunate to be born in a time and place where everyone told us to dream big. I could become whatever I wanted to. I could live wherever I wanted to. People like me had everything we needed and more. Things our grandparents could not even dream of. We had everything we could ever wish for and yet now we may have nothing. Now we probably don’t even have a future any more."',
quoteAuthor: "@GretaThunberg",
},
];
//access random quote from quote array
return quotes[Math.floor(Math.random() * quotes.length)];
};
export default getRandomQuote;Adding the Redux library
The Redux library is available from a precompiled UMD package, so I can simply add it as script to my HTML. The snippet below shows the bottom of my HTML.
Note also the type="module" used when linking index.js. Given I’m creating index.js as a JavaScript module, this is necessary to inform the browser to deal with it appropriately.
<!-- index.html -->
</footer>
<!-- adding the Redux library from a precompiled UMD package. window.Redux is the global variable to call Redux. -->
<script src="https://unpkg.com/redux@4.0.4/dist/redux.js"></script>
<script type="module" src="src/js/index.js"></script>
</body>
</html>With the library added, the UMD build makes Redux available as a window.Redux global variable. I’m calling that global variable Redux, so I can simply call the library by Redux from now on.
//index.js
// The UMD build makes Redux available as a window.Redux global variable
const Redux = window.Redux;
Action-events: events triggering actions
Back to the user stories, I want to be able to click a UI element (a button) to get a new quote. So, to make things more readable as I refer to UI elements throughout the code, I’m naming them appropriately.
//index.js
//defining UI elements
const newQuoteButton = document.getElementById("new-quote");
const quoteTextContent = document.getElementById("text");
const quoteAuthorContent = document.getElementById("author");
const tweetButton = document.getElementById("tweet-quote");
I’m creating a UI listener function tied to the newQuoteButton. This function will be dispatching actions via the newQuoteActionCreator action creator (more on action creators further down) to the Redux store (the Redux store is where the state lives) when a click event happens.
//index.js
//creating UI listeners. Dispatching actions (via the action creators that return a "type" to the reducer) to the redux store. When a new state is set in the Redux store, the store listeners will be retrieving the current state held in the Redux store
newQuoteButton.addEventListener("click", () => {
store.dispatch(newQuoteActionCreator());
});These actions, created by action creators, are simply objects that contain information about an action event that has occurred. The actions carry a type property, this property specifies the type of action that occurred.
It is common practice to write action types as const declarations.
//constants.js
//defining action types
export const NEW_QUOTE = "NEW_QUOTE";Given I’m declaring those constants in a separate constants.js module, I’m importing the const into the action creator actions.js module.
I’m also importing getRandomQuote in actions.js since I’m using it in the module.
The action creator here (newQuoteActionCreator) is a function that returns an action. It creates an object. Inside the returned action/object, I’m naming payload the key that will be associated with the object that will store the selected random quote.
//actions.js
import { NEW_QUOTE } from "../constants/constants.js";
import getRandomQuote from "../../js/js-modules/getRandomQuote.js";
//defining action creator. a function that returns an action (object that contains information about an action-event that has occurred). The action creator gets called by `dispatch()`
const newQuoteActionCreator = () => {
let quoteObject = getRandomQuote();
return {
type: NEW_QUOTE,
payload: quoteObject,
};
};
export default newQuoteActionCreator;So, when newQuoteActionCreator is called, it returns an action (which has an informative type). Another function, called reducer, makes sense of the type and informs the Redux store) how to respond to the action. In other words, the reducer tells the Redux store how to modify the state.
The reducer takes state and action as arguments and returns a new state.
//reducers.js
import { NEW_QUOTE } from "../constants/constants.js";
import getRandomQuote from "../../js/js-modules/getRandomQuote.js";
//defining initial state
const defaultQuote = getRandomQuote();
//defining reducer function to allow the Redux store to know how to respond to the action created
const getNextQuoteReducer = (state = defaultQuote, action) => {
switch (action.type) {
case NEW_QUOTE:
return {
...state,
data: action.payload,
};
default:
return state;
}
};
export default getNextQuoteReducer;Disclaimer: Use of switch...case in reducers
switch...case statements are great to show how the internals work but aren't typically used in production. You can use any conditional logic you want to write a reducer.
(Update 2021: The intention with this series is to get very incremental progress from one stack to another. Making it all as much bare bones as possible in order to get concepts adequately explored and explained. For this reason, I've covered the Redux core library (unopinionated - let's you decide how to handle everything) in the flavors covered in this series. That said, Redux Toolkit is now intended to be the standard way to write Redux logic and the recommendation is for it to be used).
As state is immutable and should never be directly modified, I’m using the object spread operator to return a new copy of the state.
The new state object has a new property: data and this property has value equal to the object associated with payload (see newQuoteActionCreator).
I still need to create the Redux store. The createStore() method) takes the getNextQuoteReducer reducer function as an argument.
//index.js
//creating the Redux store. This is where the state lives.
const store = Redux.createStore(getNextQuoteReducer);Redux application structure
As I’ve been jumping across a few JS modules in the write-up above, it can be helpful to zoom out and give a high-level view of the application’s file structure. Since this is a very simple app, I’m distributing actions, constants and reducers in different folders as opposed to following a more modular approach (bringing them together under a single folder related to every specific feature. Not following this approach since there aren’t many “features” in this application):
.
├── index.html
└── src
├── js
│ ├── index.js
│ └── js-modules
│ ├── getRandomQuote.js
│ └── getTwitterUrl.js
├── redux
│ ├── actions
│ │ └── actions.js
│ ├── constants
│ │ └── constants.js
│ └── reducers
│ └── reducers.js
└── stylesheets
└── style.cssSubscribing to the Redux store
As the application runs, actions are dispatched to the store and the state changes. The store.subscribe() method allows me to create a store listener function which is called whenever an action is dispatched to the store. I then retrieve the new state with the getState() method and re-render my UI elements with data from the new state.
//index.js
//creating store listener function that is called whenever an action is dispatched to the store. The getState() method retrieves the current state held in the Redux store
store.subscribe(() => {
//access the state of the app
const state = store.getState();
//inject random quote on HTML
quoteTextContent.innerHTML = state.data.quoteText;
//inject author on HTML
quoteAuthorContent.innerHTML = "- " + state.data.quoteAuthor;
//calling the JS module that generates a Twitter url for Twitter intent
getTwitterUrl(state.data);
});
The getTwitterUrl function called by the subscribe() method handles truncating the quote text to the adequate tweetable number of characters; generates the url for the Tweet Quote button and sets the url on the HTML. The code here follows the logic implemented in part 1 of this series.
//getTwitterUrl.js
import tweetButton from "../index.js";
//defining function that generates a Twitter URL (for Twitter intent) and inject url on HTML, making it a JS function/module
const getTwitterUrl = (quoteObject) => {
//truncating quote text in case full tweet gets to be over 280 characters
let quoteTextElem = quoteObject.quoteText;
let quoteAuthorElem = " - " + quoteObject.quoteAuthor;
let contentQuote = quoteTextElem + quoteAuthorElem;
if (contentQuote.length > 280) {
let charCountAuthor = quoteAuthorElem.length;
const extraStylingChar = "..." + '"';
let extraCharCount = extraStylingChar.length;
let subString =
quoteTextElem.substring(0, 280 - extraCharCount - charCountAuthor) +
extraStylingChar +
quoteAuthorElem;
//generate url available for Twitter intent and inject url on HTML
tweetButton.href = "https://twitter.com/intent/tweet?text=" + subString;
} else {
//generate url available for Twitter intent and inject url on HTML
tweetButton.href = "https://twitter.com/intent/tweet?text=" + contentQuote;
}
};
export default getTwitterUrl;I still need to ship one missing user story: I want to be welcomed by a quote when I first load the app. Currently, I only get a quote if I click the Get New Quote button.
I’m adding a new listener that will check for the DOMContentLoaded event that fires when the initial HTML document has been completely loaded and parsed.
//index.js
//getting initial state, a reset state as the DOM is loaded.
document.addEventListener("DOMContentLoaded", () => {
//access the state of the app
const state = store.getState();
//inject random quote on HTML
quoteTextContent.innerHTML = state.quoteText;
//inject author on HTML
quoteAuthorContent.innerHTML = "- " + state.quoteAuthor;
//calling the JS module that generates a Twitter url for Twitter intent
getTwitterUrl(state);
});
So now the random quote machine ships all the required user stories!
A visual look into the application’s execution flow
In summary, I’m changing the state in the Redux store with random quotes that get selected as the application runs. Yes, Redux updates the store with help from an action creator and a reducer, but on high-level, this is how data flows in the application: Different UI elements, such as the Get New Quote button, trigger state changes in the Redux store (with a new random quote) and a store listener function next updates the UI with the new state.
And in a diagram:
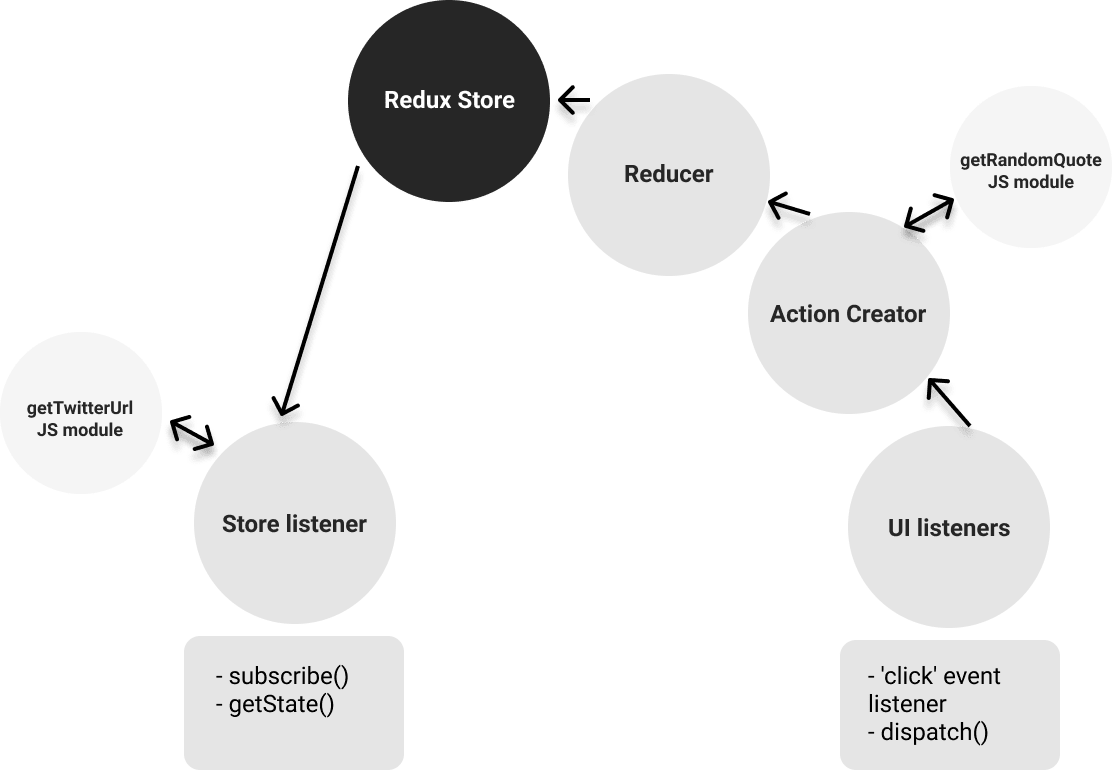
You can check the project live. Source code for flavor #4 in Github.
Acknowledgement
The following goes without saying, but here it comes anyways: Please note that in this ever changing world of technology, I am writing this article in July 2019 (hello, summer!) and alternate solutions might have become available as you read this writing.
In Part 5 (to be posted next week), I will cover a fifth flavor and will be using Redux Thunk to call an asynchronous endpoint as the data (quotes) is requested from an external resource.
If you’re curious about the next flavors, you should subscribe to Morse Wall. I think you’ll like it a lot!
So, what did you like about this post? Come say hello on Twitter!
True that...
— Morse Wall (@morsewall) August 4, 2021
There are always (at least) two ways to solve a problem. One is faster, the other you just don’t know yet.
So.. I've just added state management with Redux to an ultra simple application that could be shipped with 3 lines of functional Vanilla JS.
You are welcome 🙃 pic.twitter.com/5oNDwU7suB
Also, if you have built a random quote machine after reading this post, share it as comment to the tweet above on Twitter. Really excited to see what you create!
Happy coding!
Where to find me:
Follow me on Twitter:
You can always get my latest writings directly to your email address by subscribing to Morse Wall.
UPDATE
Part 5 of this series has now been published. Go check it out! I'm using Redux Thunk to call an asynchronous endpoint as the data (quotes) is requested from an external resource in the fifth flavor.



 by Pat
by Pat